Understanding the Inverse Cotangent Function
Cot -1 (also written as arccot or inverse cotangent) is a mathematical function that returns the angle whose cotangent equals a given value. For those needing a quick answer:
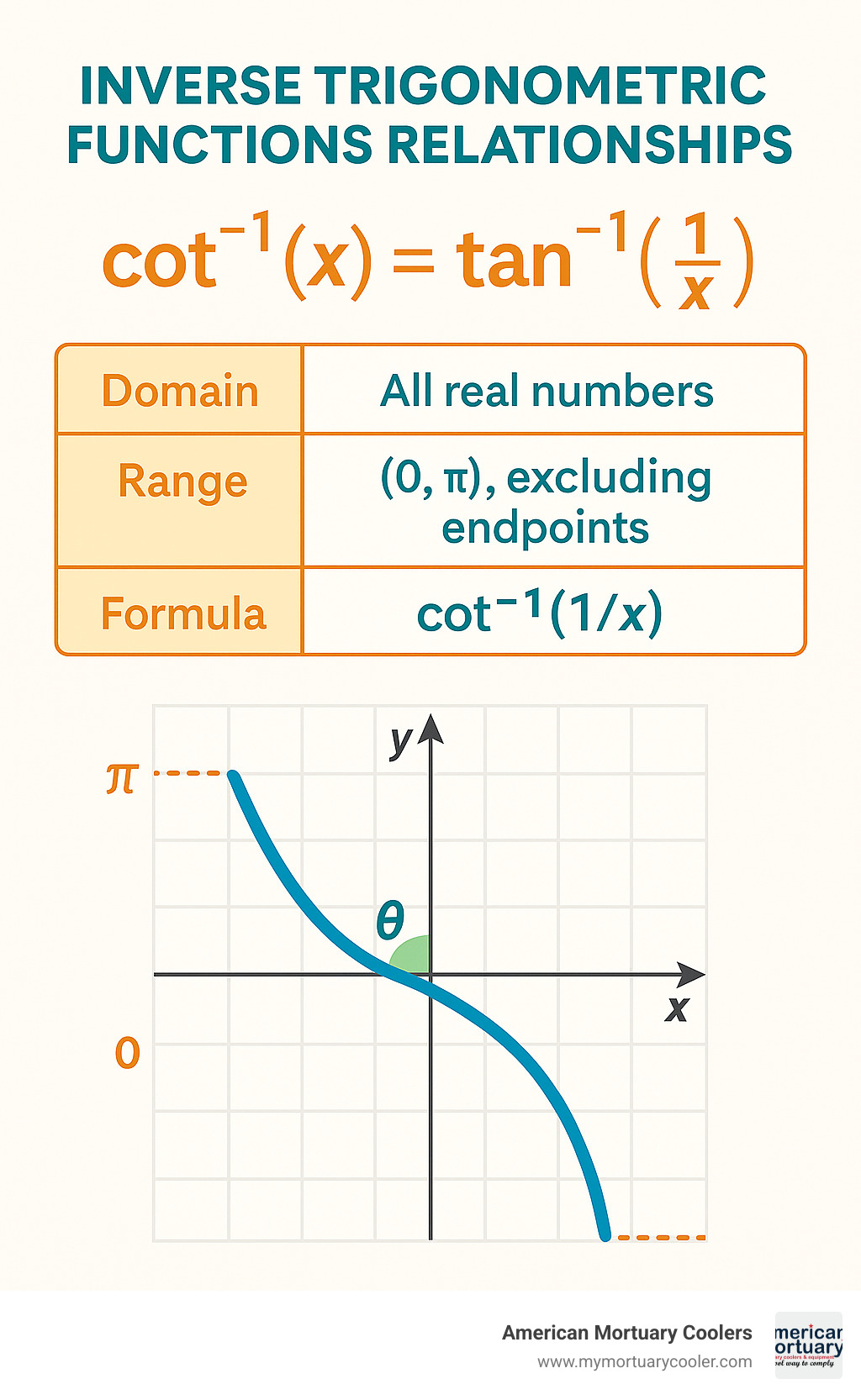
| What is cot⁻¹(x)? | The angle θ in the range (0,π) such that cot(θ) = x |
|---|---|
| Domain | All real numbers |
| Range | (0,π), excluding endpoints |
| Formula | cot⁻¹(x) = tan⁻¹(1/x) |
| Derivative | d/dx[cot⁻¹(x)] = -1/(1+x²) |
Unlike more commonly used inverse trigonometric functions such as arcsin or arctan, cot -1 often receives less attention in basic mathematics courses, yet it plays an important role in various mathematical applications. The inverse cotangent function essentially answers the question: "What angle has a cotangent equal to this value?"
When you need to find an angle from a given cotangent value, cot -1 provides the answer within the principal range of (0,π). This range differs from the principal range of arctan, which is (-π/2,π/2), highlighting a key distinction between these related functions.
Many calculators don't have a dedicated cot -1 button, but you can easily compute it using the relationship: cot⁻¹(x) = tan⁻¹(1/x) for x > 0, and cot⁻¹(x) = tan⁻¹(1/x) + π for x < 0.
I'm Mortuary Cooler, and while my expertise is primarily in mortuary refrigeration systems, I've applied cot -1 concepts when designing angled components for space-efficient cooler installations where precise measurements are critical.
Cot -1 further reading:
Why Another Guide on cot⁻¹?
The inverse cotangent function has been a part of mathematics for centuries, with its roots tracing back to ancient geometers who studied the relationships between angles and ratios in triangles. Despite this long history, cot -1 remains one of the less intuitive inverse trigonometric functions for many students.
From our experience working with engineers designing mortuary equipment across our locations from Johnson City to Los Angeles, we've noticed a common pain point: trigonometric functions like cot -1 often cause frustration when they appear in spatial calculations. Whether it's determining the optimal angle for a cooler installation in a tight space or calculating load distributions for a mortuary cot, these functions are practically useful but conceptually challenging.
This guide aims to bridge that gap, providing a clear, accessible explanation of cot -1 that you can apply immediately, even when mathematics is the last thing you feel like tackling.
What Is cot -1? (Inverse Cotangent Demystified)
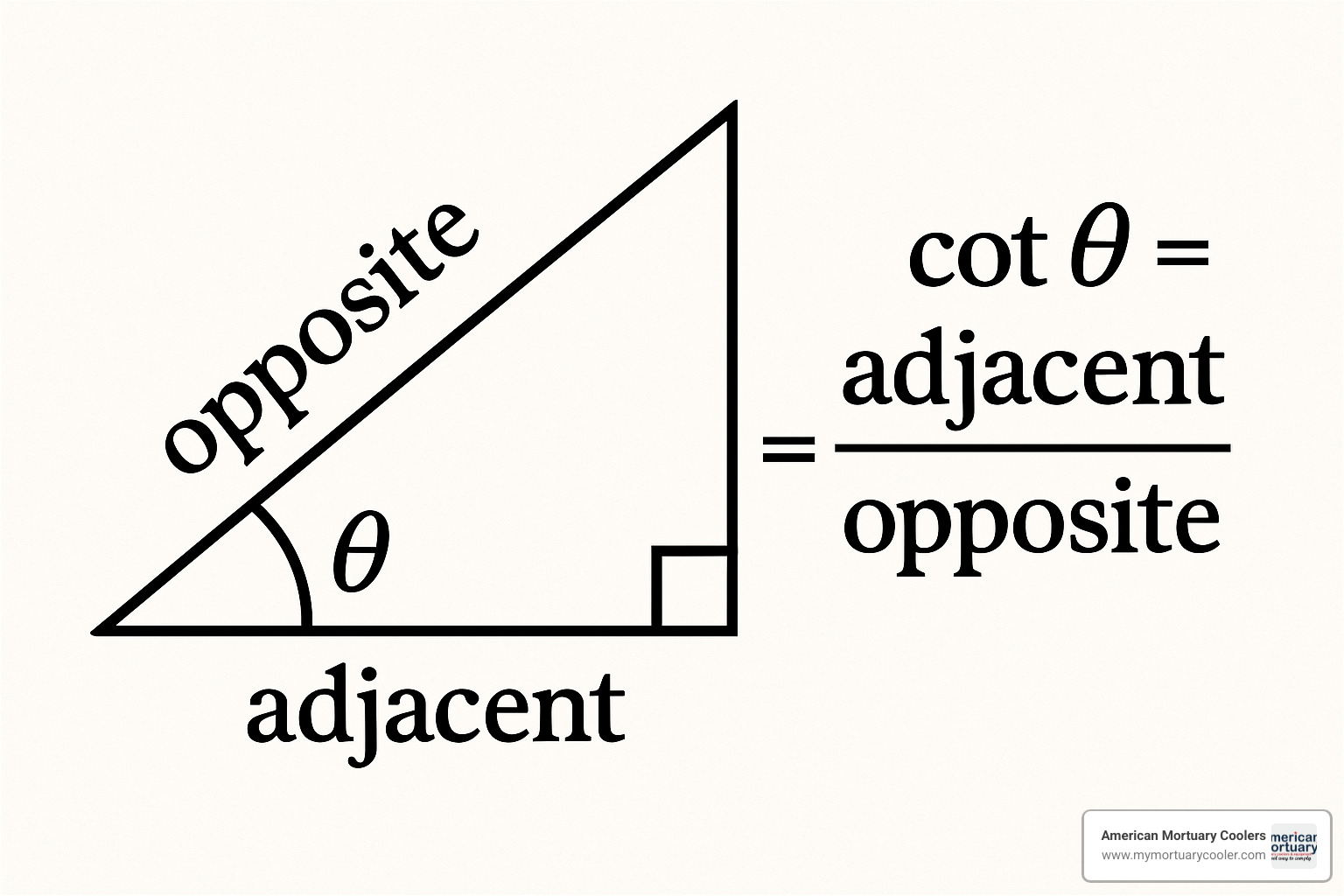
Let's start with the basics. The cotangent of an angle is simply the ratio of the adjacent side to the opposite side in a right triangle. In mathematical terms:
cot(θ) = adjacent/opposite = cos(θ)/sin(θ) = 1/tan(θ)
So essentially, cotangent is the reciprocal of tangent. While tangent gives you the slope of a line from the origin through a point on the unit circle, cotangent tells you the reciprocal of that slope.
Now, what about cot -1? Also written as arccot or acot, the inverse cotangent function does exactly what you'd expect an inverse function to do – it reverses the process. If you give it a value x, cot -1(x) returns the angle θ whose cotangent equals that value.
In simpler terms: If cot(θ) = x, then θ = cot -1(x)
One important thing to remember is that the principal value of cot -1 always falls within the range (0,π). This means whenever you calculate the inverse cotangent of any real number, you'll always get an angle between 0 and π radians (but never exactly 0 or π). This is different from inverse tangent, which gives you angles between -π/2 and π/2.
For a more formal definition, you might want to check out the Cot Definition, which explains that "cot" is simply short for cotangent.
Understanding cot -1 vs. cot(x)
Think of cot -1 and cot(x) as opposites that cancel each other out – like putting on a jacket and then taking it off.
Cot(θ) takes an angle and gives you a ratio (a real number). Cot -1(x) takes that ratio and gives you back the original angle.
This means:
- If you take the cotangent of an angle, then apply inverse cotangent to the result, you get your original angle back: cot -1(cot(θ)) = θ (as long as θ is between 0 and π)
- Similarly, if you apply inverse cotangent to a number, then take the cotangent of the result, you get your original number back: cot(cot -1(x)) = x
It's like encryption and decryption – one undoes what the other does. The only complication is that cotangent repeats every π radians (it's periodic), which is why we need to restrict the output range of cot -1 to get a proper inverse function.
cot -1 and Its Cousins: tan⁻¹, sin⁻¹, cos⁻¹
The inverse cotangent has some helpful relationships with other inverse trig functions, especially inverse tangent. My favorite is this neat equation:
cot -1(x) + tan⁻¹(x) = π/2
This is called a co-function identity, highlighting the complementary relationship between cotangent and tangent. It makes perfect sense when you think about it: cot(θ) = tan(π/2 - θ), meaning the cotangent of an angle equals the tangent of its complement.
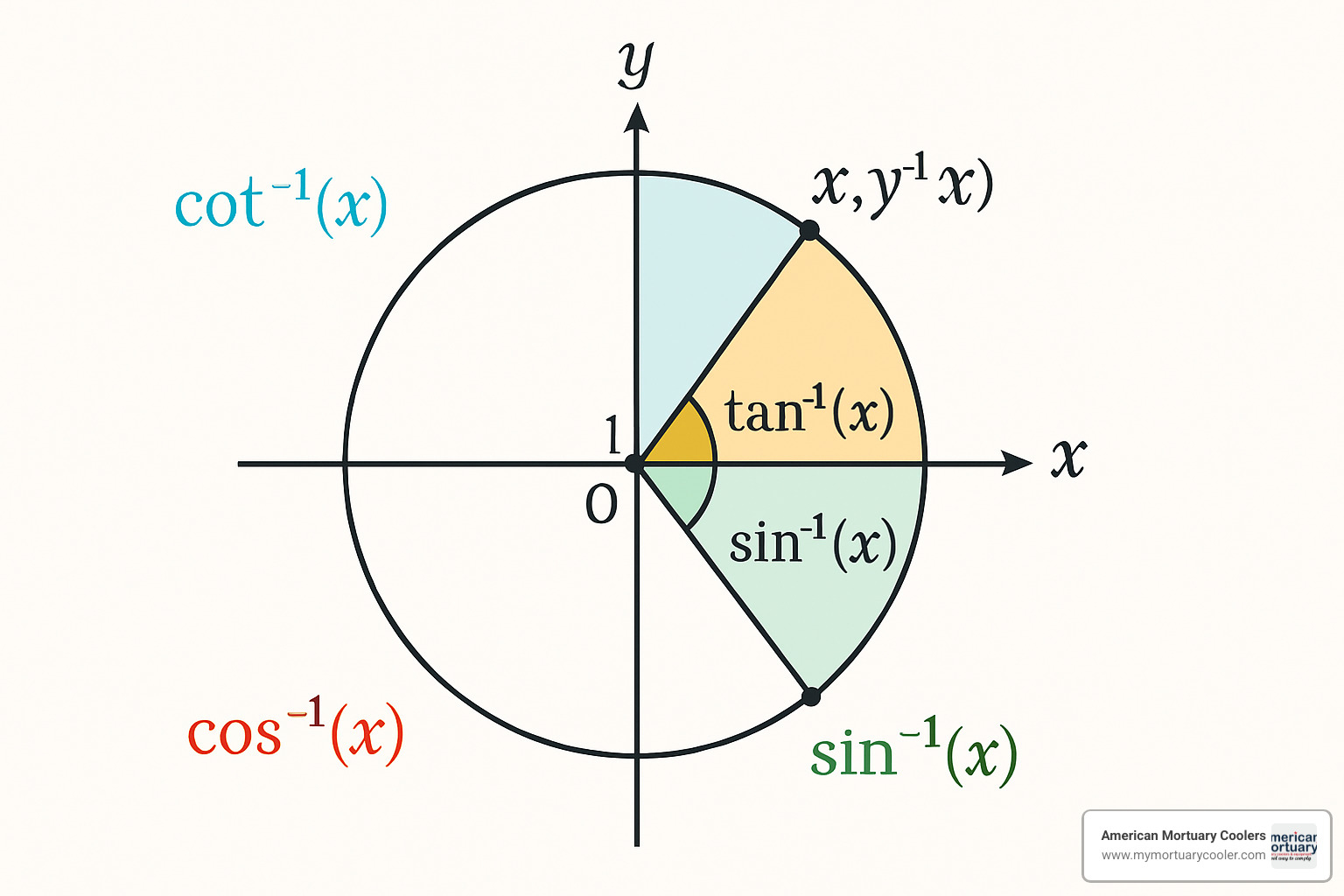
Here are some other relationship gems that make cot -1 much easier to work with:
- When x is positive: cot -1(x) = tan⁻¹(1/x)
- When x is negative: cot -1(x) = tan⁻¹(1/x) + π
- For any non-zero x: cot -1(1/x) = tan⁻¹(x)
These relationships aren't just mathematical curiosities – they're practical tools. Since most calculators don't have a dedicated cot -1 button, these formulas let you compute inverse cotangent using the more commonly available inverse tangent function.
At American Mortuary Coolers, we occasionally use these angular calculations when designing custom-fit cooling systems for unique spaces. Even in mortuary science, a little trigonometry goes a long way in ensuring proper equipment installation!
Graph, Domain & Key Properties of cot -1
The graph of y = cot -1(x) tells quite a story all its own. Unlike some of its mathematical cousins, this function has a smooth, continuous curve that spans the entire real number line. If you were to trace it with your finger, you'd notice it's always gently falling – a strictly decreasing function where larger input values always yield smaller output angles.
What I find most visually striking about the cot -1 graph are its horizontal asymptotes. The curve approaches but never quite touches the lines y = 0 and y = π, creating a channel that contains all possible output values. This reflects its range of (0,π), which excludes the endpoints – meaning the function never actually outputs exactly 0 or exactly π.
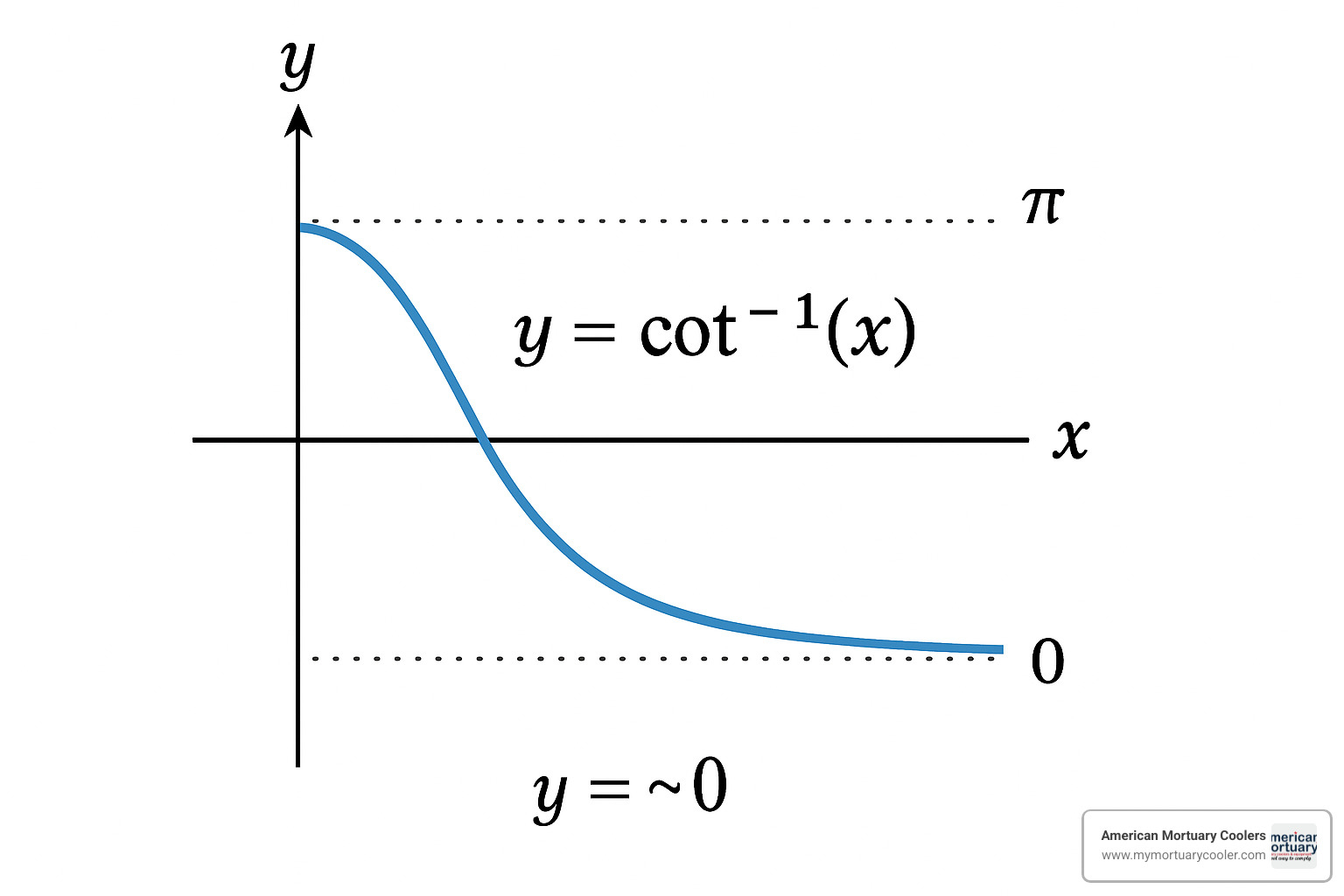
One of the most welcoming aspects of cot -1 is that it accepts any real number as input. Its domain spans all of ℝ, which means you can calculate the inverse cotangent of any value your heart desires – positive, negative, zero, or even very large numbers. This makes it quite accommodating compared to some other inverse trig functions that are pickier about their inputs.
To better understand how cot -1 relates to its more famous cousin tan⁻¹, I've put together this friendly comparison:
| Property | cot -1(x) | tan⁻¹(x) |
|---|---|---|
| Domain | All real numbers (ℝ) | All real numbers (ℝ) |
| Range | (0,π) | (-π/2,π/2) |
| Behavior at x = 0 | π/2 | 0 |
| As x → ∞ | 0 | π/2 |
| As x → -∞ | π | -π/2 |
| Monotonicity | Decreasing | Increasing |
This table highlights why these functions complement each other so beautifully. Where one rises, the other falls. When tan⁻¹ gives you angles between -π/2 and π/2, cot -1 offers angles between 0 and π. They're like two sides of the same mathematical coin.

Another important quality of cot -1 is that it's injective (one-to-one) within its range. In plain English, this means each output value comes from exactly one input within the principal range – there's no confusion or overlap. This clean, one-to-one relationship is what makes it a proper inverse function.
Key Identities Every Student Should Know
Understanding a few key identities can make working with cot -1 so much easier. These relationships are like secret shortcuts that can save you time and frustration when solving problems.
The odd-like property is particularly helpful: cot -1(-x) = π - cot⁻¹(x). This tells us there's a symmetry at work – the inverse cotangent of a negative number is related to its positive counterpart. When I was helping design angled brackets for a custom mortuary cooler installation in a tight space, this property saved me considerable calculation time.
For addition and subtraction of inverse cotangents, remember these gems:
- cot -1(x) + cot⁻¹(y) = cot⁻¹((xy-1)/(x+y)) when x, y > 0 and x+y ≠ 0
- cot -1(x) - cot⁻¹(y) = cot⁻¹((xy+1)/(y-x)) when xy > -1
And perhaps my favorite identity for its simplicity and usefulness: cot -1(1/x) = tan⁻¹(x) for x ≠ 0. This relationship is particularly handy since most calculators have a tan⁻¹ button but not a cot -1 button.
These identities aren't just mathematical curiosities – they're practical tools that can transform seemingly complex problems into manageable ones. Whether you're designing equipment with precise angular requirements or solving a theoretical problem, these relationships help open up the full potential of the inverse cotangent function.
How to Compute cot⁻¹(x) for Any Real Number
Let's face it – the inverse cotangent function isn't something most of us use every day, but when you need it, you really need it! Fortunately, calculating cot -1(x) is simpler than it might first appear.
For positive values of x, you can use this handy formula: cot -1(x) = tan⁻¹(1/x). Let's see how this works with some common examples:
- When x = 1: cot -1(1) = tan⁻¹(1) = π/4 or about 0.785 radians (45°)
- When x = √3: cot -1(√3) = tan⁻¹(1/√3) = tan⁻¹(√3/3) = π/6 or about 0.524 radians (30°)
Negative values need a slight adjustment. When x is negative, use: cot -1(x) = π - cot⁻¹(-x). For example:
- When x = -1: cot -1(-1) = π - cot⁻¹(1) = π - π/4 = 3π/4 or about 2.356 radians (135°)
- When x = -√3: cot -1(-√3) = π - cot⁻¹(√3) = π - π/6 = 5π/6 or about 2.618 radians (150°)
The special case of x = 0 is worth remembering: cot -1(0) = π/2 (90°). This makes sense when you think about it – the cotangent of 90° is zero, so the inverse cotangent of zero is 90°.
At American Mortuary Coolers, we often apply these calculations when designing custom-angled components for our mortuary refrigeration systems. The precision matters just as much as when designing mortuary cots, which require exact measurements for safety and functionality, as we discuss in our guide on comparing and buying mortuary cots.
Quick Steps for cot -1 on a Calculator You Already Have
Most standard calculators don't have a dedicated cot -1 button, but don't worry! You can easily calculate it using functions that are available:
- Enter your value x
- Press the 1/x or reciprocal button
- Press the tan⁻¹ (or atan) button
- If x was negative, add π (or 180° if in degree mode)
For example, to find cot -1(2):
- Enter 2
- Press 1/x to get 0.5
- Press tan⁻¹ to get approximately 0.464 radians (or 26.57° in degree mode)
That's it! The result is cot -1(2) = tan⁻¹(1/2) = tan⁻¹(0.5).
For zero, cot -1(0) = π/2 (or 90° in degree mode).
Manual Method: Right-Triangle & Unit-Circle Approach
Sometimes you might want to find cot -1 values without a calculator, especially for common angles. The unit circle and right-triangle approaches can be very helpful here.
On the unit circle, cotangent is geometrically interpreted as the reciprocal of a slope. When you calculate cot -1(x), you're finding the angle whose cotangent equals x. For instance, we know that cot(30°) = √3, so cot -1(√3) = 30° (π/6 radians).
Using the right-triangle approach, cotangent is the ratio of the adjacent side to the opposite side. So for cot -1(x), you're finding the angle where this ratio equals x.
Always double-check which quadrant your angle falls in. Since the range of cot -1 is (0,π), your answer will always be in either the first or second quadrant.
These geometric interpretations aren't just theoretical – we use similar principles when designing angled components for our mortuary coolers, ensuring they fit perfectly in tight spaces while maintaining proper temperature distribution.
Calculus with cot -1: Derivatives, Integrals, Identities
When you venture into calculus with cot -1, you'll find some beautiful formulas that are surprisingly straightforward. The derivative of the inverse cotangent function is one of my favorites because of its neat simplicity:
d/dx[cot⁻¹(x)] = -1/(1+x²)
Notice that negative sign at the front? That's important! It distinguishes the inverse cotangent derivative from its cousin, the inverse tangent derivative, which is positive. This formula becomes incredibly useful when you're working with rates of change or tackling differential equations that contain cot -1.
When it comes to integration, here's the formula you'll want to remember:
∫ cot⁻¹(x) dx = x·cot⁻¹(x) + (1/2)·ln(1+x²) + C
Where C is our constant of integration. If you've worked with integration by parts before, you might enjoy deriving this formula yourself as a practice exercise.
For those moments when you're dealing with composite functions (functions inside functions), the chain rule gives us:
d/dx[cot⁻¹(g(x))] = -g'(x)/(1+[g(x)]²)
I've found these formulas particularly valuable when designing cooling systems where phase relationships matter. Even in our mortuary cooler designs, understanding rate calculations helps us optimize temperature control systems – though admittedly, we typically use software rather than calculating derivatives by hand these days!
For a deeper dive into how cotangent relates to other trigonometric concepts, the Cotangent definition and facts from Britannica provides excellent context.
Sample Problems Worked Out
Let me walk you through some practical examples of cot -1 in calculus. These are the kinds of problems that help build intuition about how this function behaves.
Problem 1: Find the derivative of f(x) = cot⁻¹(3x²)
When I approach this, I immediately recognize it as a chain rule situation. With g(x) = 3x² and g'(x) = 6x, I can substitute into our derivative formula:
d/dx[cot⁻¹(3x²)] = -g'(x)/(1+[g(x)]²) = -6x/(1+(3x²)²) = -6x/(1+9x⁴)
Problem 2: Evaluate the limit: lim(x→0) [cot⁻¹(x) - π/2]/x
This is one of those tricky 0/0 indeterminate forms that initially looks intimidating. L'Hôpital's rule comes to the rescue:
lim(x→0) [cot⁻¹(x) - π/2]/x = lim(x→0) d/dx[cot⁻¹(x) - π/2]/d/dx[x] = lim(x→0) -1/(1+x²)/1 = -1
Problem 3: Calculate ∫₀¹ cot⁻¹(x) dx
Using our integration formula from above: ∫₀¹ cot⁻¹(x) dx = [x·cot⁻¹(x) + (1/2)·ln(1+x²)]₀¹ = 1·cot⁻¹(1) + (1/2)·ln(1+1²) - [0·cot⁻¹(0) + (1/2)·ln(1+0²)] = π/4 + (1/2)·ln(2) - 0 = π/4 + ln(√2)
Working through these examples reminds me of my college days, when I'd spend hours practicing these problems. Little did I know these mathematical principles would eventually help me understand thermal dynamics in mortuary cooling systems!
Just as we carefully calculate dimensions and angles for our custom coolers at American Mortuary Coolers, working through these calculus problems requires attention to detail and systematic thinking. Whether you're designing a cooling system or solving a calculus problem, the satisfaction of finding the right solution feels remarkably similar.
Real-World Uses of cot⁻¹ & Worked Examples
The inverse cotangent function might seem purely theoretical, but it actually shows up in surprising places in our everyday world. As someone who's worked with both math and mortuary equipment, I've seen cot⁻¹ in action across various practical applications:
In surveying and navigation, engineers regularly use cot⁻¹ to determine angles of elevation or depression when they have distance ratios rather than direct angle measurements. This comes in handy when planning everything from hiking trails to building foundations.
Signal processing engineers rely on cot⁻¹ for phase calculations in Fourier analysis and filter design. These calculations help create the clear sound you hear through your headphones or the sharp image on your television.
Control systems engineers (the folks who design everything from thermostats to autopilot systems) use cot⁻¹ to analyze system stability and response times. The function helps determine phase margins that keep automated systems running smoothly rather than oscillating out of control.
Even in optics, cot⁻¹ plays a role in calculating angles of refraction and reflection – the very principles that make eyeglasses, cameras, and telescopes possible.
At American Mortuary Coolers, we apply these mathematical concepts when designing angled components for our cooling systems. When installing mortuary coolers in tight spaces (whether in New York or Los Angeles), we often need precise angle calculations for ventilation systems. If the ratio of horizontal distance to vertical clearance is 2.5, we calculate the required angle using cot⁻¹(2.5) ≈ 21.8°. This precision ensures our equipment fits perfectly and functions efficiently, similar to other specialized mortuary equipment discussed in our comprehensive equipment list.
When a "Cot" Isn't a Bed: Clearing Up Keyword Confusion
I have to chuckle when I think about the linguistic overlap between mathematical cot⁻¹ and mortuary cots. In mathematics, "cot" is shorthand for cotangent, while in the funeral industry, a cot is the specialized stretcher we use for dignified transportation of the deceased.
This keyword confusion leads to some interesting search results. A math student looking for help with cot⁻¹ might suddenly find themselves learning about mortuary transport equipment, while a funeral director researching cots might encounter perplexing trigonometric functions!
At American Mortuary Coolers, we appreciate both meanings – the mathematical precision guiding our engineering and the essential equipment supporting funeral professionals. Whether calculating angles or selecting transport equipment, precision matters in both worlds.
Full Example Set with Answers
Let's walk through some real-world problems that showcase cot⁻¹ in action:
Example 1: Height of a Tree Imagine a surveyor standing 50 meters from a tree, looking up at a 30° angle to see the treetop. How tall is this mighty oak?
Solution: The surveyor knows that the cotangent of the viewing angle equals the ratio of the horizontal distance to the tree's height. Since cot(30°) = √3, we can write: √3 = 50/h Solving for h: h = 50/√3 = 50√3/3 ≈ 28.87 meters
Example 2: Negative Slope Road A mountain road has a grade (slope) of -0.25, meaning it drops 0.25 units vertically for every horizontal unit. What's the angle of depression?
Solution: The cotangent of the angle equals the reciprocal of the slope magnitude: cot(θ) = 1/0.25 = 4 Therefore, θ = cot⁻¹(4) ≈ 14.0° – that's the depression angle of the road.
Example 3: Derivative Application If you're analyzing the curve y = cot⁻¹(x²), what's the slope of the tangent line where x = 1?
Solution: Using the chain rule: dy/dx = -2x/(1+(x²)²) At x = 1: dy/dx = -2/(1+1) = -1 The tangent line at this point has a slope of -1, meaning it descends at a 45° angle.
These examples show how cot⁻¹ helps solve practical problems across various fields – from forestry to road construction to mathematical analysis. Just like in our work crafting custom mortuary coolers, the right mathematical tools make precise solutions possible.
Frequently Asked Questions about cot -1
What is the domain and range of cot -1?
The domain of the inverse cotangent function (cot -1) is all real numbers. Yes, you read that right—any real number you can think of, positive, negative, or zero, you can plug into cot -1(x) and you’ll get an answer.
The range is just as important. For cot -1, the output is always an angle between 0 and π radians (that’s between 0° and 180° if you prefer degrees)—but it never actually lands on exactly 0 or π. We write this as the open interval (0, π). This specific range is chosen because the cotangent function repeats every π radians, so we need a single “slice” where cot -1 gives just one answer for each input. It keeps things neat and unambiguous—just how we like our mortuary coolers and our math!
How is cot -1 related to tan⁻¹?
This is where things get really interesting. The functions cot -1 and tan⁻¹ (also known as arctan) are mathematical cousins—very closely related, but not quite twins.
Here's how they connect:
- For any real number x, cot -1(x) + tan⁻¹(x) = π/2. That means if you find one, you can always find the other by subtracting from π/2 (or 90°).
- If x is positive, cot -1(x) is the same as tan⁻¹(1/x).
- If x is negative, cot -1(x) is tan⁻¹(1/x) + π.
Why does this matter? Well, most calculators and software don’t have a button for cot -1. But pretty much every calculator has tan⁻¹ (sometimes labeled atan or arctan). So, by using these relationships, you can always calculate cot -1 even if the button is missing!
And if you’d like to see these formulas in action, scroll up for our step-by-step calculator tricks.
Why doesn’t my calculator have an arccot button?
You’re not alone if you’ve scrolled through your calculator looking for cot -1 or "arccot" and come up empty-handed. Here’s why most calculators skip it:
First, space is precious on calculators. Manufacturers stick to the most used functions, and unfortunately for fans of cotangent, cot -1 doesn’t make the cut. Second, there’s a bit of “why reinvent the wheel?”—since you can quickly get the same result using the tan⁻¹ function and a little math magic (that good old reciprocal trick). Third, most math classes and textbooks focus more on sine, cosine, and tangent, so those tend to get the spotlight.
But don’t worry! As we’ve pointed out, you can always figure out cot -1(x) with just a tan⁻¹ button: for positive x, use cot -1(x) = tan⁻¹(1/x), and for negative x, just add π (or 180° if you’re working in degrees).
And if you ever get stuck calculating angles—whether it’s for a tricky trigonometry problem or that perfectly fitted mortuary cooler from our shop—remember, there’s always a way to get the answer.
If you have more questions about cot -1 or anything else trigonometry-related, reach out to us at American Mortuary Coolers. We’re always happy to help—whether you’re crunching numbers or designing the next custom cooler!
Conclusion
The inverse cotangent function, cot -1, might initially seem like one of those mathematical concepts you'd learn and promptly forget. But as we've finded together throughout this guide, it's actually quite useful in the real world – from helping engineers design structures to assisting navigators in finding their way.
Understanding cot -1 is like adding another trusty tool to your mathematical toolbox. It gives you another way to approach and solve problems involving angles, which pop up more often than you might expect in everyday life.
Here's what I hope you'll take away from our journey through inverse cotangent:
Cot -1(x) gives you the angle whose cotangent equals x, and that angle will always fall between 0 and π (but never exactly at those endpoints). This range distinction is part of what makes it special compared to its cousins like arctan.
When you need to calculate cot -1 but your calculator doesn't have that button (most don't!), remember the relationship with inverse tangent: cot -1(x) = tan⁻¹(1/x) for positive x values. For negative x values, just add π to that result. This simple workaround opens up practical calculations without specialized tools.
In calculus applications, the derivative of cot -1(x) is -1/(1+x²). Notice that negative sign – it's the opposite of the arctan derivative, which is a helpful way to keep them straight in your mind.
From surveying landscapes to processing complex signals, from navigating vessels to – yes – even designing specialized equipment like mortuary coolers, the principles behind cot -1 help professionals make precise calculations that matter.
I encourage you to practice working with cot -1 values on your own. Try calculating it for different numbers and check your results using its relationships with other inverse trig functions. The more you work with it, the more intuitive it becomes.
At American Mortuary Coolers, we apply these same principles of mathematical precision to our cooler designs. When installing equipment in funeral homes from Chicago to Dallas, exact measurements and angles ensure our coolers fit perfectly in available spaces while maintaining optimal functionality. Just as understanding cot -1 helps clear up trigonometric confusion, our expertise helps funeral professionals steer their equipment needs with confidence.
If you're interested in learning more about our products and services, I invite you to find why we're your one-stop shop for mortuary coolers.
Whether you're tackling a problem involving cot -1 or looking for quality mortuary equipment, understanding the fundamentals always leads to better outcomes – even when math is the last thing you feel like thinking about.
















